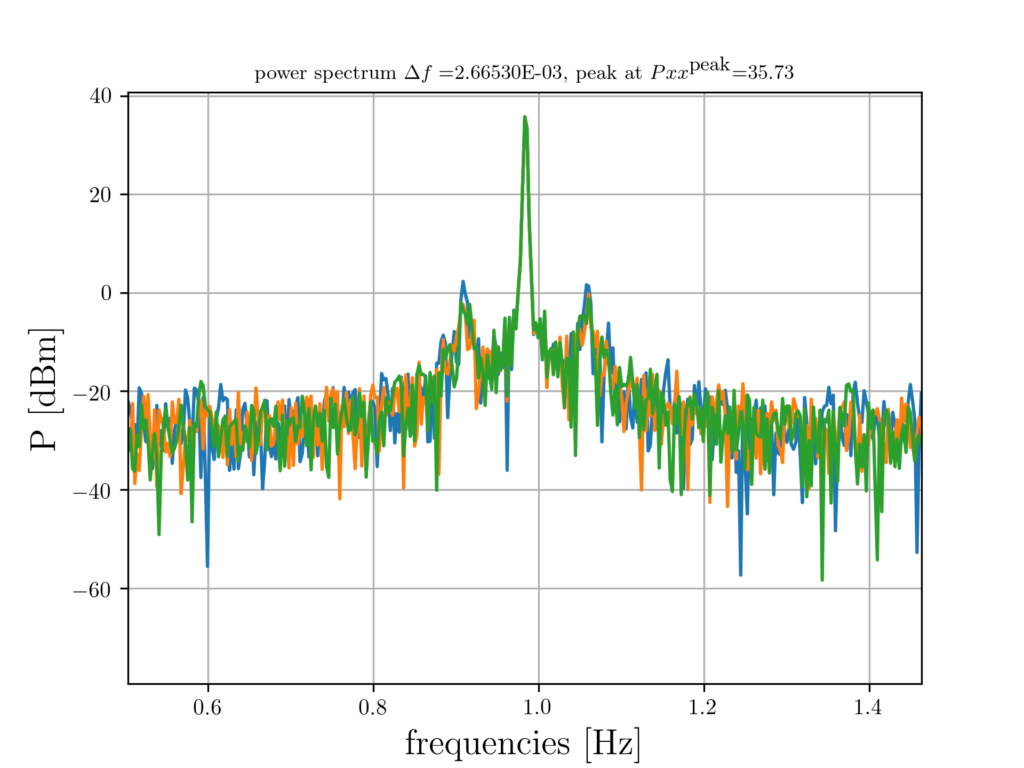
Self-organized synchronization in mutually delay-coupled electronic clocks
Electronic systems rely on large numbers of components that perform tasks in a concerted way. For instance, the localization precision of indoor and outdoor positioning systems (GPS, GLONASS, Galileo) is directly related to the quality of time-synchronization of their units. State-of-the-art solutions to synchronization use a hierarchical approach, in which a high quality reference-clock corrects spatially distributed low quality clocks. We study a novel approach to synchronization in electronic systems that relies on the self-organization of synchronized states.
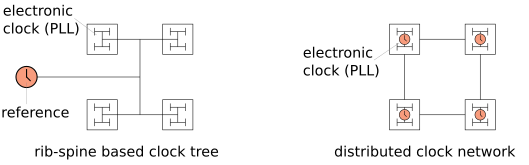
We study how systems of mutually coupled electronic clocks, so called phase-locked loops (PLLs), enable synchronous clocking in large-scale systems with transmission time delays. We use a phase description of PLL networks that includes signal filtering and delayed signal transmission.
We showed in theory and experiment that transmission delays in the coupling enable the existence of stable synchronized states, while instantaneously coupled PLLs do not tend to synchronize to zero phase-difference and analyzed how filtering and transmission delay time-scales govern the collective frequency and the time scale of synchronization.
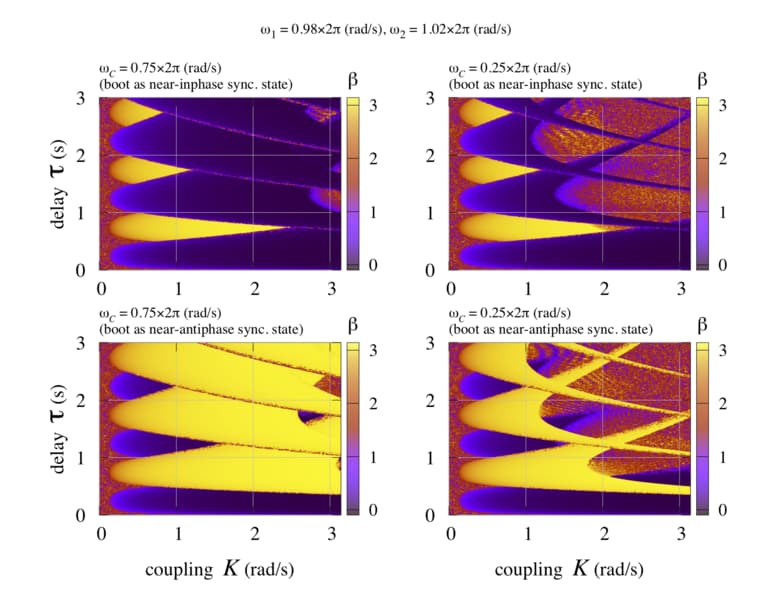
How clock heterogeneity affects synchronization
The production process of integrated metal-oxide semiconductor based microelectronics inherently leads to highly heterogeneous components on the circuit level. Since it is not feasible to characterize all individual components in modern electronic architecture designs, these need to be robust against such heterogeneity. We study the effects of electronic clock component heterogeneity on the synchronization dynamics and the properties of self-organized synchronized states.
Basin stability of synchronized states in mutually delay-coupled oscillator networks
Dynamical systems theory provides powerful tools to characterize the dynamics of complex systems. These include for example the calculation and characterization of synchronized states and the computation of their stability against small perturbations.
Analyzing the response of such systems against large perturbations however is not a simple task. We use Lp-Adaptation to estimate the basins of attraction of synchronized states in large networks of mutually delay-coupled electronic clocks. With this we can estimate which type of perturbation will break the desired operational state of the system.
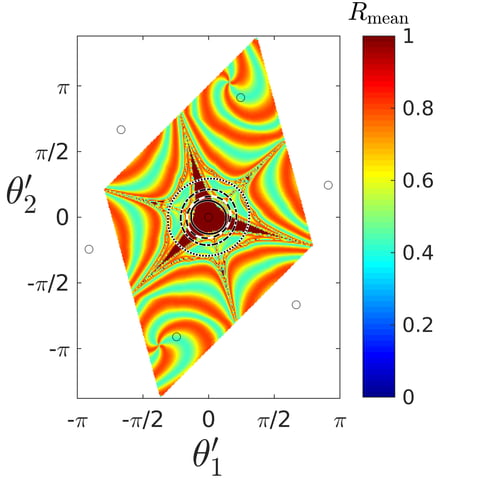
Control of self-organized synchronization in electronic clock networks
To enable self-organization in engineered systems it is necessary to control its dynamics. This requires a detailed understanding of how the intrinsic system parameters are connected to the dynamics of the system. Then control can be achieved by tuning these parameters and thereby guiding the self-organized dynamics to the desired regimes.
Noise in networks of mutually delay-coupled phase-locked loops
Oscillator systems are subject to intrinsic and extrinsic noise which impacts the quality of their oscillations. In coupled system, the individual oscillator noise affects synchronization and the quality of synchronized states. Also, there are natural boundaries to how much the contributions of noise in such systems can be reduced. Is synchronization even possible in systems of coupled electronic clocks at very large frequencies? Using different approaches we study the effects of noise on synchronization and the stability of synchronized states.